Section 8.2 Laboratoire
Dans ce laboratoire, on s’intéresse au type de lien qui peut exister entre deux variables quantitatives. Plus spécifiquement, on cherche à déterminer l’existence d’un lien linéaire entre des variables \(X,Y\text{,}\) et donc de l’existence de coefficients \(a,b\) pour lesquels \(Y\approx aX+b\text{.}\) Cette droite est appelée la droite de régression. Cette droite est appelée la droite de régression. Plus la dépendance entre \(X,Y\) est forte, plus cette approximation sera bonne. La force de ce lien (linéaire) est donnée par le coefficient de corrélation, aussi appelé coefficient de Pearson. Il est noté \(r\) dans le cas d’un échantillon et \(\rho\) (lettre grecque « rho ») pour une population.
La première étape d’une étude sur la nature du lien entre deux variables doit toujours être l’observation des données afin de vérifier qualitativement la plausabilité de l’existence d’un lien linéaire entre les variables. L’équation de la droite de régression ainsi que le coefficient de corrélation peuvent presque toujours être calculés, même si les données ne sont pas reliées linéairement. Il incombe à l’analyste de déterminer la pertinence et l’interprétation adéquate de ces outils.
Pour présenter ces concepts, on utilise une base de données portant sur \(421\) étoiles de type « céphéide ». Une céphéide est une étoile variable, c’est-à-dire dont la luminosité change dû à un mouvement périodique de dilatation et de contraction. La première à avoir été découverte, par l’astronome amateur John Goodricke en 1784, fait partie de la constellation Céphée, qui a par la suite prêté son nom à cette nouvelle catégorie d’étoile. Les données datent de \(1997\) et proviennent de l’Observatoire-David-Dunlap à Richmond Hill, en Ontario. Cet observatoire a été désigné comme un lieu historique national en 2019. Les variables présentes dans le fichier sont
1
www.astro.utoronto.ca/DDO/research/cepheids/cepheids.html2
parcs.canada.ca/culture/designation/lieu-site/david-dunlap- ID: Numéro de l’échantillon
- Étoile: Nom de l’étoile
- Période: Période de pulsation (en jours)
- Mag App: Magnitude apparente moyenne (sans unités)
- Couleur BV: Indice de couleur B-V moyen (sans unités)
- Excès: Excès de couleur (sans unités)
- Amplitude V: Amplitude de la luminosité observée au travers d’un filtre V (~500nm) (sans unités)
- Mag Abs: Magnitude Absolue (sans unités)
- Dist: Distance entre l’étoile et le soleil (parsecs)
- VR MOY: Vitesse radiale moyenne (km/s)
- RAYON: Rayon solaire ( x 6,957x10^8 m)
Sous-section 8.2.1 Corrélation et régression linéaire
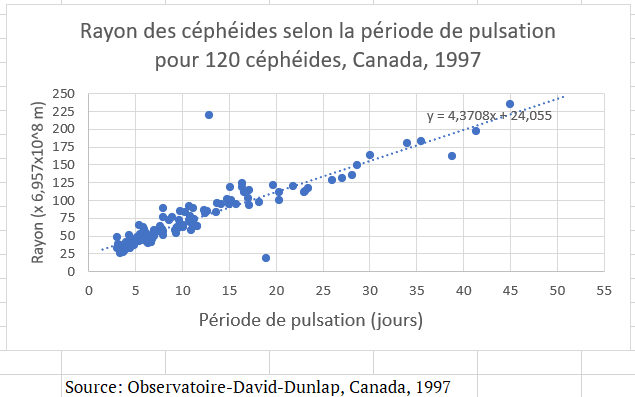
Dans le prélaboratoire, on a demandé de tracer le nuage de points de la période de pulsation en fonction du rayon. À l’observation du graphique, il est plausible de conclure à l’existence d’un lien linéaire entre le rayon d’une céphéide et sa période de pulsation. On peut donc aller de l’avant avec l’analyse de la relation linéaire entre ces variables.
Dans un premier temps, on calcule le coefficient de corrélation linéaire. La formule
COEFFICIENT.CORRELATION(matrice1;matrice2) permet d’obtenir ce coefficient, où matrice1 et matrice2 sont les plages contenant les données des deux variables. La formule mathématique du coefficient de corrélation est
\begin{equation}
r=\frac{1}{n-1}\sum_{i=1}^n\left(\frac{x_i-\bar{x}}{s_x}\right)\left(\frac{y_i-\bar{y}}{s_y}\right).\tag{8.2.1}
\end{equation}
C’est une mesure de la variabilité conjointe des variables, normalisée pour être entre \(-1\) et \(1\text{.}\)
Le signe du coefficient de corrélation donne le sens de la variabilité de la variable \(Y\) lorsque \(X\) varie: une variation positive de \(X\) entraine une variation positive de \(Y\) lorsque \(r>0\) et une variation positive de \(X\) entraine une variation négative de \(Y\) lorsque \(r<0\text{.}\) La magnitude du coefficient de corrélation quant à elle quantifie la force du lien linéaire entre les variables. Traditionnellement, la force est obtenue selon la valeur de \(|r|\) dans la table suivante. TODO AJUSTER AVEC MANUEL
| \(|r|\) | Interprétation du lien |
| \(]0,8;1]\) | Très fort à parfait |
| \(]0,6;0,8]\) | Fort |
| \(]0,4;0,6]\) | Modéré |
| \(]0,2;0,4\) | Faible |
| \([0;0,2]\) | Aucun à très faible |
On calcule le coefficient de corrélation entre la période de pulsation et le rayon des céphéides et on l’ajoute sous les études descriptives. Puisque les écarts types des variables font partie de la formule mathématique (8.2.1) du coefficient de variation, ce dernier est sensible aux valeurs extrêmes. Il est donc important de bien analyser les données lors d’une étape préliminaire.
Une fois la nature linéaire du lien confirmée, il est possible de déterminer l’équation de la meilleure droite qui relie les deux variables. L’exercice Activité 8.1.2 donne une idée de la procédure mathématique à suivre pour la trouver. Un ouvrage statistique théorique peut montrer que la pente est donnée par \(a=r\frac{s_y}{s_x}\) et l’ordonnée à l’origine par \(b=\bar{y}-a\bar{x}\text{.}\) Sur Excel, on peut afficher directement sur le graphique la droite et son équation. Pour cela, on sélectionne le graphique et on clique sur la petite croix en haut à droite, puis sur linéaire. La case Courbe de tendance aurait aussi pu faire le travail, puisque son comportement par défaut est la relation linéaire. Pour ajouter l’équation, on clique sur Autres options ou on fait un double-clic sur la droite créée précédemment et on coche la case Afficher l’équation sur le graphique.
La fonction
DROITEREG permet aussi d’obtenir directement dans les cellules les valeurs de \(a,b\text{,}\) mais elle a comme inconvénient qu’il faut que le nombres de valeurs pour chacune des variables soit le même. Dans le cas de la base de données des céphéides, le rayon de plusieurs étoiles est manquant. Il faut alors filtrer dans la formule pour exclure les entrées vides. La formule DROITEREG((FILTRE(PÉRIODE;Rayon<>0));(FILTRE(RAYON;RAYON<>0))) permet d’accomplir cela, où PÉRIODE et RAYON sont les plages nommées correspondant à ces variables dans le tableau des données. Dans les deux cas, si l’on note \(P\) la période et \(R\) le rayon, on obtient
\begin{equation}
P=0,184600309R-2,250611573\text{.}\tag{8.2.2}
\end{equation}
Avec cette droite, on est en mesure d’estimer la période de pulsation d’une céphéide de rayon donné ou à l’inverse, de déterminer le rayon d’une étoile dont la période de pulsation est connue. Par exemple, la céphéide FF_AQL dont l’identifiant est \(4\) possède une période égale à environ \(4,47\) jours. En entrant cette valeur dans l’équation, on estime un rayon de \(36,41124772(x6,957x10^8)\) mètres. Selon Wikipédia, la composante numérique du rayon est de 39.
3
en.wikipedia.org/wiki/FF_Aquilae#cite_note-turner-5Une autre mesure de la force du lien est donnée par le coefficient de détermination, habituellement noté \(R^2\) (sans lien avec le rayon mentionné précédemment). Ce dernier quantifie la proportion des variations de la variable dépendante qui sont expliquées par la variable indépendante. Il est donné en pourcentage et lorsqu’il n’y a qu’une seule variable indépendante, on a toujours
\begin{equation*}
R^2=r^2\times 100\%\text{.}
\end{equation*}
Sur excel, la commande
COEFFICIENT.DETERMINATION(matrice1;matrice2) permet de l’obtenir, mais ne donne pas le résultat en pourcentage. Il faut manuellement modifier le format de cellule. En calculant le coefficient de détermination entre la période de pulsation et le rayon d’une céphéide, on trouve qu’une variation du rayon d’une étoile de type céphéide explique environ \(81\%\) de la variation de sa période de pulsation.Sous-section 8.2.2 Absence de lien linéaire apparent et autres cas
Dans la feuille MappP, on trace le nuage de points représentant la magnitude apparente et la période de pulsation. Le résultat est illustré à la figure ci-dessous.
Le calcul des coefficients de corrélation et de détermination montre d’autant plus que ces variables ne sont pas reliées de manière linéaire. Ceci s’explique probablement en partie du fait que la luminosité apparente dépend de la distance de l’étoile. Au contraire, la magnitude absolue ramène cette valeur sur une même échelle.
Dans la feuille MabsP, on trace le nuage de points représentant la magnitude absoulue et la période de pulsation. Le résultat est illustré à la figure ci-dessous.
Deux choses ressortent de ce graphique. Premièrement, la relation ne semble pas linéaire, mais il y a clairement un lien entre les deux variables. Deuxièmement, bien que la relation semble très forte, il semble aussi y avoir deux types de relations. En effet, on peut observer dans le graphique produit deux amas principaux de points. Ces deux amas paraissent suivre une relation de même type, mais il y a possiblement une troisième variable qui influence le lien entre la magnitude absolue et la période de pulsation, ou des erreurs dans les données disponibles.
On commence par s’attarder à la première observation. Bien qu’elle ne soit pas linéaire, la relation liant les variables ressemble à un courbe bien connue, soit un logarithme. En cliquant sur l’outil croix du graphique, puis sur la flèche au niveau de l’option courbe de tendance suivi de autres options, on peut modifier le type de fonction utilisée pour approximer le lien. L’option logarithme est présente. On peut également afficher l’équation sur le graphique, qui sera de la forme \(a\ln(x)+b\text{.}\)
Une autre option est de modifier l’axe de la période pour que l’échelle soit logarithmique. Voici la marche à suivre pour y arriver.
- Faire un clic à l’aide du bouton de droite de la souris sur l’axe de la période, ou encore effectuer un double-clic;
- Dans le menu apparaissant, cliquer sur le petit icone ressemblant à un histogramme et appelé Options d’axe.
- Cocher la boite appelée Échelle logarithmique.
Pour la deuxième observation, déterminer la nature de la cause relèverait davantage de la physique que des statistiques. Il existe deux types de céphéides, pour lesquels la période et la magnitude absolue suivent en effet des relations différentes, mais toutes deux logarithmiques, mais une analyse des données a montré que la presque totalité des étoiles de cette base de données sont de type \(I\text{.}\)
Le calcul du coefficient de détermination linéaire pour ces deux variables est relativement fort. Par contre, dans les options de la courbe de tendance, il est possible de faire calculer le coefficient de détermination de la relation logarithmique, qui est encore plus fort. Afficher ce coefficient sur le graphique.

