Définition 7.3.1. Noyau de floutage simple.
Une matrice \(N\in\mathcal{M}_{(2n+1)\times (2n+1)}\) où chaque entrée vaut \(\frac{1}{(2n+1)^2}\) est appelé un noyau de floutage simple dans le contexte du traitement d’image. Par exemple, les matrices
\begin{align*}
N_3&=\begin{pmatrix}
\frac{1}{9}&\frac{1}{9}&\frac{1}{9}\\
\frac{1}{9}&\frac{1}{9}&\frac{1}{9}\\
\frac{1}{9}&\frac{1}{9}&\frac{1}{9}\\
\end{pmatrix}\\
N_5&=\begin{pmatrix}
\frac{1}{25}&\frac{1}{25}&\frac{1}{25}&\frac{1}{25}&\frac{1}{25}\\
\frac{1}{25}&\frac{1}{25}&\frac{1}{25}&\frac{1}{25}&\frac{1}{25}\\
\frac{1}{25}&\frac{1}{25}&\frac{1}{25}&\frac{1}{25}&\frac{1}{25}\\
\frac{1}{25}&\frac{1}{25}&\frac{1}{25}&\frac{1}{25}&\frac{1}{25}\\
\frac{1}{25}&\frac{1}{25}&\frac{1}{25}&\frac{1}{25}&\frac{1}{25}\\
\end{pmatrix}
\end{align*}
sont deux noyaux de floutage, respectivement d’ordre \(3\) et \(5\text{.}\)
Pour les entrées sur le bord de la grille, il n’y a pas nécessairement neuf voisins. Dans ces cas, on prend remplace la valeur des voisins absents par
\(0\text{.}\) L’animation suivante montre le processus complet de l’application du noyau sur la grille de l’image précédente.
Calcul 7.3.4. Floutage par noyau simple.
On propose de flouter la couverture du manuel à l’aide d’un noyau simple d’ordre 3. Dans un premier temps, on doit charger l’image. La cellule suivante est identique à celle se trouvant dans le texte ci-haut.
Pour le moment,
\(G\) est une matrice de taille
\(200\times 155\text{.}\) Afin de pouvoir appliquer le floutage sur l’ensemble de ces valeurs, il est utile d’ajouter un contour de zéros à cette matrice afin de pouvoir appliquer le noyau sans se soucier des bords. On appelle ce procédé le bourrage. Pour cela, la commande
block_diagonal_matrix peut être utile. Celle-ci permet de créer une matrice en définissant les blocs se retrouvant le long de la diagonale principale. Sage complètera la matrice afin qu’elle soit de la bonne taille en ajoutant des zéros. En anglais, cet ajout de zéros se nomme “padding”. Voici un exemple simple avant de l’appliquer sur la matrice
\(G\text{.}\)
Dans le cas de la couverture du manuel, on veut simplement encadrer la matrice
\(G\) de zéros. On peut procéder comme suit.
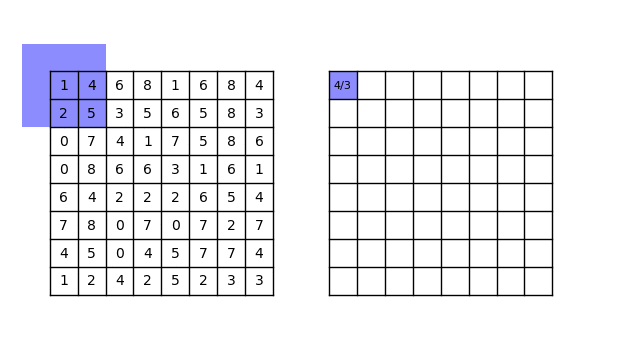
Pour appliquer le floutage, on doit calculer la moyenne de chaque pixel de la matrice
\(G\) et de ses voisins immédiats. Dans la cellule précédente, on voit le coin supérieur gauche de la matrice modifiée. Dans ce cas, la moyenne du premier pixel et de ses vosins est de
\(103.55556\text{.}\) On doit convertir les entrées de la matrices en liste afin de calculer la moyenne.
On crée une fonction qui prend comme argument une paire de nombres
\(i,j\) et une matrice
Gpad et retourne la moyenne de l’entrée en position
\(i,j\) et de ses voisins immédiats dans la matrice . On s’assure également que l’argument ne peut pas être au bord de la matrice.
Enfin, on crée la nouvelle matrice formée de ces moyennes. À noter le décalage nécessaire puisque le pixel correspondant dans la matrice
Gpad se trouve une ligne et une colonne plus loin.
On peut assez bien distinguer l’image originale de celle qui a subi le floutage, bien que l’effet soit subtil. Pour obtenir un meilleur effet, on pourrait appliquer à nouveau le floutage. L’exercice
[provisional cross-reference: exo-fctplusieurspassage] permet d’explorer cette possibilité.
Une autre option consiste à augmenter la taille du noyau de floutage. Il faut également penser à augmenter la taille du bourrage effectué. On commence par créer une fonction qui prend une matrice et un entier
\(n\) comme arguments et effectue un bourrage d’ordre
\(n\text{.}\) On rappelle que selon la définition
7.3.1,
\(n\) doit être un nombre impair. Si
\(n=2k+1\text{,}\) alors il faut ajouter à la matrice
\(k\) lignes et colonnes de chaque côté.
La prochaine étape consiste à modifier la fonction
noyausimple afin qu’elle soit modulable selon la valeur
\(n\) du noyau. La nouvelle version prend comme arguments la matrice de l’image originale
\(G\) ainsi que l’ordre du noyau
\(n\text{.}\)
Finalement, on crée la fonction qui permet de flouter une image
\(G\) selon un noyau d’ordre
\(n\) impair.
La cellule ci-dessous permet de comparer l’effet de l’ordre de floutage sur l’image originale de manière interactive.
Lorsque la taille du noyau augmente, il est légitime de se demander si le fait d’attribuer autant de poids aux pixels éloignés du centre est la chose à faire. Dans une image haute résolution, plus on s’éloigne d’un pixel, plus les chances sont que les couleurs (ou dans ce cas-ci, les tons de gris) soit différentes augmentent. On peut alors utiliser un noyeau pondéré.
Il est commun d’avoir un étalement symétrique des poids alloués aux pixels, comme dans les noyaux de l’exemple
7.3.6, mais ce n’est pas strictement nécessaire. L’effet pourrait toutefois être disproportionné.
Un noyau de floutage pondéré particulièrement utile est le noyeau Gaussien. Les valeurs du noyau sont déterminées selon la distribution de la loi normale, aussi appelée distribution gaussienne. Cette distribution statistique donne un poids plus grand au centre et attribue un poids proportionnellement plus petits aux valeurs éloignées. La loi normale dépend de deux paramètres, la moyenne
\(\mu\) et l’écart type
\(\sigma\text{,}\) mais pour le noyau de floutage, seul l’écart type est nécessaire. Celui-ci va définir l’intensité du floutage. Voici la représentation de quelques courbes de la loi normale ainsi que leur valeur pour
\(\sigma\text{.}\)
Comme on travaille en deux dimensions, il faut considérer l’équation de la loi normale pour deux variables. Celle-ci, pour une moyenne égale à zéro, est donnée par l’équation
\begin{equation}
\frac{1}{\sqrt{2\pi \sigma}}e^{-\frac{(x^2+y^2)}{2\sigma^2}}\text{.}\tag{7.3.1}
\end{equation}
Pour construire le noyau gaussien, il est pratique de créer une fonction intermédiaire de déphasage permettant à l’entrée au centre d’une matrice d’être considéré comme le point \((0,0)\text{.}\) Les coordonnées des autres entrées de la matrice sont données en relation de leur distance horizontale et verticale avec le centre. Le code suivant donne la fonction de déphasage à utiliser ainsi que son effet sur les entrées d’une matrice \(n\times n\text{.}\)
En théorie, tous les points contribuent à la moyenne d’un noyau gaussien, même ceux très éloignés. En pratique, il n’y a que les points situés à une distance de plus ou moins six sigmas qui auront une contribution significative. Deux choix sont possibles pour la suite. On peut fixer la taille du noyau et renormaliser en divisant par la somme des données. On peut également déterminer la taille du noyau à utiliser en fonction de l’écart type. On prendra l’entier impair plus grand que
\(6\sigma+1\text{,}\) afin qu’il y ait
\(6\) écarts types de part et d’autre de l’entrée au centre. Pour alléger les calculs, il est parfois possible de réduire ce facteur
\(6\text{,}\) en gardant au minimum
\(3\text{.}\) Dans ce qui suit, on opte pour l’option de déterminer la taille selon l’écart type. La cellule ci-dessous crée une fonction qui retourne le noyeau gaussien d’écart type
sigma de dimension correspondant à plus ou moins
nbr écarts types.
Maintenant qu’on a le noyau, il faut l’appliquer à la matrice image. Pour un noyau simple, il suffisait de faire la somme des entrées autour du centre et diviser par le carré de la dimension du noyau. Avec un noyau pondéré, il faut passer par l’étape intermédiaire où l’on multiplie chaque entrée autour du centre dans la matrice image par son poids relatif dans le noyau. Ce n’est pas aussi simple que de passer par la multiplication matricielle, puisqu’au final on veut obtenir une seule valeur pour chaque centre de l’image. La fonction suivante modifie la fonction de floutage simple pour tenir en compte de ce calcul. Attention, un écart type trop grand fera en sorte que les fonctions ci-dessous ne seront pas en mesure de s’exécuter dans un temps appréciable.